Even though quite small, the tablet of YBC 7289 contains one of the most famous mathematical texts from ancient Mesopotamia, a civilization that flourished between the fourth millennium BCE and the early first millennium AD, in what is now the Republic of Iraq. The original tablet is housed in the Yale Babylonian Collection at Yale University in New Haven, Connecticut, USA. It most likely comes from southern Iraq, but its exact provenance is unknown. It can be dated to the 19th or 18th century BCE. The tablet was scanned and digitized (Figure 1) at Yale’s Institute for the Preservation of Cultural Heritage.

Figure 1: image of the original YBC 7289 Babylonian tablet getting scanned in a Reflectance Transformation Imaging (RTI) dome
.
The tablet has a round shape that is typical for texts written by Babylonian students who learnt how to write and calculate in cuneiform, the script used by Mesopotamian scribes and scholars. Tablets thus formed were known in Babylonian as imšukkum, i.e., “hand tablet,” because they fit comfortably in the student’s palm.
The tablet shows a square with both diagonals drawn in (Figure 2). A number sign on the upper left indicates that the sides of the square are each 30 units long. Along the diagonal, we find the numerals 1,24,51,10 and 42,25,35, both written, in accordance with the conventions of the Babylonian sexagesimal system, to base 60. The second of these numbers indicates the length of the diagonal; it can be read as 42 × 1 + 25 × 1/60 + 35 × 1/3600, or 42.426389. The first number, converted to a decimal, gives 1.414212963, which is very close to √2, that is, 1.414213562. Apparently, the student, to find out the length of the diagonal of a square whose sides were each 30 units long, had calculated 30 × [1;24,51,10], which yields 42;25,35.
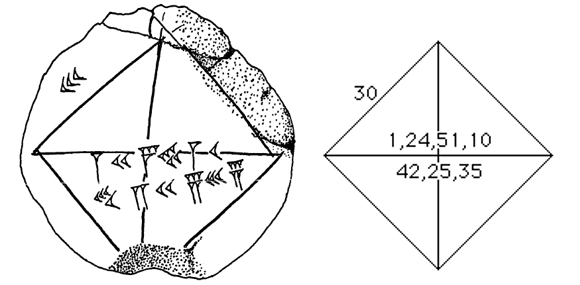
Figure 2: Explanatory drawing of YCB 7289
.
The tablet proves that the Babylonians of the early second millennium BCE knew that the ratio of the side to diagonal in a square is 1 to the square root of 2. They had come to this insight long before the Greek philosopher Pythagoras, who probably lived in the sixth century BCE, established his famous theorem a2 + b2 = c2, which is behind their solution. The tablet demonstrates, moreover, that the mathematicians of the Old Babylonian era had found a remarkably good approximation to √2: 1;24,51,10. The student who wrote the tablet seems to have taken this number from a list of coefficients (one such list is likewise housed in the Yale Babylonian Collection).
The literati of ancient Mesopotamia excelled in many scholarly disciplines, including medicine and lexicography. But their mathematical knowledge was particularly sophisticated and advanced, and predated comparable achievements among the Greeks by many centuries.
The 3D-print was produced from data obtained at Yale IPCH within the Yale Babylonian Collection Digital Imaging Project, drawing on the 107-year-old, 45,000 object Yale Babylonian Collection as one of the most important collections of Mesopotamian tablets and other artifacts in the Western Hemisphere. The main goals of the project were to produce high quality material for adoption in scholarly research and education as well as to formulate and perfect acquisition and data management techniques.
Methods of digitization adopted in this project included reflectance transformation imaging (RTI), 3D laser scanning, multispectral imaging (MSI) and high-resolution photography. The final products of these digital acquisitions comprise interactive visualizations, 3D models and high quality images.
We hope that this collaborative project serves to increase access, unites the existing metadata with the new visualizations and furthers the expansion of research methodologies into cuneiform digitization projects at Yale and beyond.
Further reading:
D.H. Fowler and E. Robson, “Square root approximations in Old Babylonian mathematics: YBC 7289 in context,” Historia Mathematica 25 (1998), 366-78.
Asger Aaboe, “Episodes from the Early History of Mathematics”, Washington, D.C.: Mathematical Association of America (MAA), 1998 (originally published in 1964), 25-27.